CMR-rep
Timothy B. Terriberry
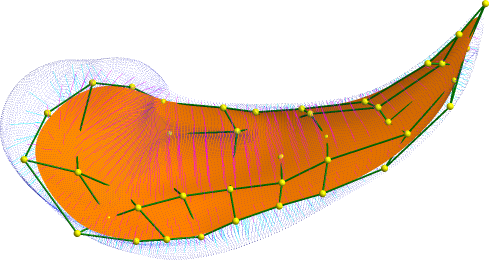
This is a public release of the source code that accompanies my
Ph.D. thesis, where I developed a new, continuous 3-D
medial shape model for biological objects.
This model is based on Catmull-Clark subdivision surfaces and represents a
shape using a continuous, analytically evaluatable medial axis.
It offers some improvements over previous work in this area by
Paul Yushkevich, on
which it is based:
-
Branch curve boundary conditions can be enforced, allowing the connection of
multiple medial sheets while maintaining a smooth, closed surface.
This allows the representation of a much richer set of medial topologies than a
single medial sheet, and can be used to model a much larger class of objects.
This is the first continuous medial model to support branching.
-
Edge curve boundary conditions required to ensure a smooth, closed surface
around the edge of a medial sheet can be enforced along a specific curve in
the sheet's parametric domain.
This is essential in order to be able to do statistics on populations of
medially described objects.
Paul's original work enforced these boundary conditions on an implicit curve
which had to be solved for, and was different for every model.
-
The control point mesh can contain vertices of arbitrary valence.
This allows the construction of meshes which are not regular grids and which do
not directly correspond to rectangular parameter domains.
This provides much greater modeling flexibility and allows the use of more
control points in more complicated areas of the shape and fewer control
points in simpler areas.
Like Paul's original work, the model can be evaluated using fast spline
techniques.
Most patches on the medial sheet are B-splines, and those near extraordinary
vertices can be transformed into B-splines via a well-known eigenbasis
decomposition due to Jos Stam.
Patches which enforce boundary conditions are still B-splines along one
dimension.
Paul's later work was able to solve the problem of enforcing the edge boundary
conditions at a specific location by solving a differential equation at finely
sampled discrete locations over the whole medial sheet.
We can evaluate any point on the surface directly in constant time.
Qiong Han is currently developing
another continuous medial representation based on the radial shape operator
defined by Jim Damon.
It requires numerical integration across the entire surface to evaluate the
model, but has the intriguing feature that it can ensure models are
legal—that is, that the object surface does not overfold on
itself—by construction.
Both our work and Paul's work require that legality be enforced during model
optimization, by subsampling it to a sufficient resolution when deforming it
to fit a target shape and checking a set of legality conditions.
Qiong's work is, however, still in progress, and currently limited to a single
medial sheet.
Downloads
- Win32 Binaries
- Source Code
-
No tarballs are currently available, but those who are interested are
encouraged to access the subversion repository directly:
Selected Publications
-
Timothy B. Terriberry:
Continuous
Medial Models in Two-Sample Statistics of Shape.
PhD thesis, University of North Carolina at Chapel Hill, Department of Computer
Science, December 2006.
[slides]
-
Timothy B. Terriberry, and
Guido Gerig:
"A
Continuous 3-D Medial Shape Model with Branching."
In Proceedings of the International Workshop on Mathematical Foundations of
Computational Anatomy (MFCA'06), pp. 80–89, Copenhagen, Denmark,
October 2006.
[slides]
-
Timothy B. Terriberry,
James N. Damon,
Stephen M. Pizer,
Sarang C. Joshi, and
Guido Gerig:
"Population-based
Fitting of Medial Shape Models with Correspondence Optimization."
In Nico Karssemeijer and
Boudewijn P.F. Lelieveldt,
editors, Proceedings of the 20th International Conference on
Information Processing in Medical Imaging (IPMI'07), volume 4584 of
Lecture Notes in Computer Science, pp. 700–711, Kerkrade, The
Netherlands.
Springer-Verlag, July 2007.
[poster]
Related Publications
-
Yushkevich, Paul A.:
Statistical
Shape Characterization Using the Medial Representation.
PhD thesis, University of North Carolina at Chapel Hill, 2003.
-
Yushkevich, Paul A.,
Hui Zhang, and
James
C. Gee:
"Parametric Medial Shape
Representation in 3-D via the Poisson Partial Differential Equation with
Non-linear Boundary Conditions."
In Gary E. Christensen and
Milan Sonka, editors,
Proceedings of the 19th International Conference on Information
Processing in Medical Imaging (IPMI'05), volume 3565 of Lecture Notes
in Computer Science, pp. 162–173, Glenwood Springs, Colorado.
Springer-Verlag, July 2005.
-
Qiong Han,
Stephen M. Pizer, and
James N. Damon:
"Interpolation in
Discrete Single Figure Medial Objects."
In Proceedings of the IEEE Computer Society Workshop on Mathematical Methods
in Biomedical Image Analysis (MMBIA'06), pp. 209–216, New York City,
New York, June 2006.
